 Exercice 1
Exercice 1
En 1990, Monsieur Dufisc a fait sa première déclaration d'impôt sur le revenu :
il a déclaré un revenu annuel de 90 000 francs, l'impôt correspondant s'est
élevé à 8 000 francs et son revenu après impôt a donc été de 82 000 francs.
Chacune des quatre années suivantes, son revenu annuel a augmenté de 2% et
l'impôt correspondant a augmenté de 3%.
Monsieur Dufisc souhaite étudier ce qu'il adviendrait de son revenu après
paiement de l'impôt si l'évolution constatée se poursuivait.
Dans ce but, on suppose que l'évolution constatée se poursuit et, pour tout
entier n positif ou nul, on note :
 Rn
le montant, exprimé en francs, du revenu annuel de Monsieur Dufisc en l'an (1990
+ n),
Rn
le montant, exprimé en francs, du revenu annuel de Monsieur Dufisc en l'an (1990
+ n),
 In
le montant, exprimé en francs, de l'impôt correspondant,
In
le montant, exprimé en francs, de l'impôt correspondant,
 Un
= Rn - In, le revenu après impôt. (R0 = 90 000,
I0 = 8 000, U0 = 82 000)
Un
= Rn - In, le revenu après impôt. (R0 = 90 000,
I0 = 8 000, U0 = 82 000)
1. a) Calculer R1, I1, U1,
R2, I2, U2.
b) Montrer que, pour tout entier positif n, on a
:
Rn = 90 000×(1,02)n
In = 8 000×(1,03)n
2. a) Montrer que, pour tout entier positif n,
Un+1 - Un = 1 800×(1,02)n - 240×(1,03)n.
b) Montrer que : Un+1 < Un
équivaut à
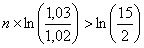 .
.
c) Déterminer les entiers positifs n qui
vérifient
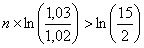 .
.
3. Si l'évolution que Monsieur Dufisc a constatée
concernant son revenu et l'impôt correspondant se poursuit, Monsieur Dufisc
verra-t-il son revenu après l'impôt diminuer ?
 Exercice 2
Exercice 2
Depuis qu'il est à la retraite, un homme tond sa pelouse tous les samedis, il
recueille chaque fois 120 litres de gazon qu'il stocke dans un bac à compost de
300 litres.
Chaque semaine les matières stockées perdent, après décomposition ou prélèvement
les trois quarts de leur volume.
Soit V1, V2, V3 les volumes en litres stockés
respectivement les premier, deuxième et troisième samedis après la tonte.
De manière générale, soit Vn le volume stocké le nième
samedi après la tonte.
1. a) Montrer que V1 = 120 litres, V2
= 150 litres, V3 = 157,5 litres.
b) Calculer les volumes V4, V5,
V6 exprimés en litres, stockés respectivement les quatrième,
cinquième, sixième samedis après la tonte.
2. Exprimer Vn+1 en fonction de Vn.
3. On définit, pour tout n 1,
tn par : tn = 160 - Vn.
1,
tn par : tn = 160 - Vn.
a) Montrer que (tn) est la suite
géométrique de premier terme t1 = 40 et de raison
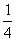 .
.
b) En déduire les expressions de tn
puis de Vn en fonction de n.
c) Déterminer la limite de (tn) puis
celle de (Vn).
 Exercice 3
Exercice 3
Au premier janvier 1995, une ville A compte 200 000 habitants. A la même date
une ville B a 150 000 habitants.
On a constaté que la population de la ville A diminue de 3% par an et que celle
de la ville B augmente de 5% par an.
Dans cet exercice, on suppose que les croissances et les diminutions se
poursuivent à ce rythme.
1. Quelles seront les populations des villes A et B
au premier janvier 1996 ? au premier janvier 1997 ?
2. Pour tout entier n, on désigne par : an
la population de la ville A au premier janvier de l'année (1995 + n) et par bn
la population de la ville B à la même date.
a) Vérifier que les suites (an) et (bn)
sont géométriques. Préciser leurs raisons respectives.
b) Exprimer an et bn en
fonction de n.
c) Au premier janvier de cette année, la
population de la ville B sera-t-elle, pour la première fois, supérieure à celle
de la ville A ?
CORRECTION
 Exercice 1
Exercice 1
Pour tout entier naturel n, on pose :
Rn le montant, en francs, du revenu annuel de M. Dufisc en l'an 1990
+ n
In le montant de l'impôt correspondant
Un = Rn - In le revenu de M. Dufisc après
impôt.
1. a) Le revenu annuel augmente de 2% par an,
donc : R1 = R0 + (2/100)×R0, soit R1
= 1,02 R0.
Donc : R1 = 91 800 francs.
Un an plus tard, ce revenu a encore augmenté de 2%, donc :
R2 = 91 800 + 91 800×(2/100) = 1,02 R1, soit R2
= 93 636 francs.
L'impôt augmente de 3% par an, donc :
I1 = 8 000 + (3/100)×8 000 = 8 000×1,03, soit I1 = 8
240 francs.
I2 = I1 + (3/100)×I1 = 8 240×1,03, soit I2
= 8587,20 francs.
Ainsi, nous avons:
U1 = R1 - I1 = 83 560 francs.
U2 = R2 - I2 = 85 148,80 francs.
b) Soit n un entier positif quelconque. Le
revenu annuel augmente de 2% par an, donc à l'année (1990 + n + 1) le revenu Rn+1
est donné par Rn+1 = Rn + (2/100)×Rn = 1,02Rn.
(Rn) est donc une suite géométrique de raison 1,02 et de premier
terme R0 = 90 000.
Ainsi, pour tout entier naturel n, Rn = 90 000×(1,02)n.
Pour tout entier n, le montant In+1 de l'impôt à l'année (1990 + n+
1) a augmenté de 3% par rapport à celui de l'année (1990 + n).
Nous avons donc : In+1 = In + (3/100)×In =
1,03In.
La suite (In) est donc géométrique de raison 1,03 et de premier terme
I0 = 8 000.
Par suite, pour tout entier n, In = 8 000×(1,03)n.
2. a) Pour tout entier naturel n, Un+1
- Un = (Rn+1 - In+1) - (Rn - In)
= 90 000×(1,02 - 1)×(1,02)n - 8 000×(1,03 - 1)×(1,03)n
= 1 800×(1,02)n - 240×(1,03)n.
b) Pour tout entier n, Un+1<Un
équivaut à Un+1 - Un<0
c'est-à-dire 1 800×(1,02)n - 240×(1,03)n<0, soit 1
800×(1,02)n<240×(1,03)n
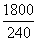 <
<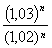 ,
c'est-à-dire :
,
c'est-à-dire :
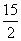 <
<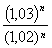 .
.
Donc : ln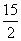 <ln
<ln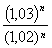 car la fonction ln est strictement croissante sur ]0 ; +
car la fonction ln est strictement croissante sur ]0 ; + [.
[.
Donc : ln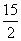 < n ln
< n ln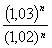 .
.
c) Nous avons ln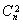 >0,
donc n ln
>0,
donc n ln
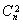 >
ln
>
ln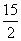 équivaut à :
équivaut à :
n >
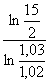 = 206,5 à 0,1 près.
= 206,5 à 0,1 près.
Les entiers n vérifiant n ln
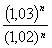 >ln
>ln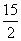 sont donc les entiers n supérieurs ou égaux à 207.
sont donc les entiers n supérieurs ou égaux à 207.
3. Nous avons montré à la question précédente
que Un+1<Un pour tout entier n supérieur ou égal à 207,
c'est-à-dire que la suite (Un) est décroissante à partir du terme de
rang 207.
M. Dufisc ne verra donc pas son revenu après impôt diminuer (Celui-ci diminuera
en l'an 1990 + 207 = 2197).
 Exercice 2
Exercice 2
1. a) Soit Vn le volume en litres stocké
dans le bac le nième samedi.
Le premier samedi, il a recueilli 120 litres, donc V1 = 120 litres.
Le deuxième samedi, les ¾ de ce qui était stocké s'est décomposé ou a été
prélevé ; il restait donc 120×¼ = 30 litres avant la tonte (de 120 litres).
Au total, le second samedi, le volume est : V2 = 30 + 120 litres,
soit V2 = 150 litres.
De la même manière, les ¾ du volume stocké ont disparu la semaine suivante ; il
reste donc dans le bac 150×¼ = 37,5 litres, auxquels se rajoutent les 120 litres
de la tonte. Ainsi, le troisième samedi, le volume est V3 = 157,5
litres.
b) De la même manière, nous avons V4
= 157,5+ 120, soit V4 = 159,375 litres.
V5 = 159,375×¼ + 120, soit V5 = 159,844 litres.
V6 = 159,844 ×¼ + 120, soit V6 = 159,961 litres.
2. Soit n un entier naturel. Le volume stocké à
la (n + 1)-ième semaine est composé :
- du quart du volume stocké la semaine précédente ;
- des 120 litres de la tonte de la pelouse.
Il s'ensuit que nous avons Vn+1 = Vn + 120.
3. Pour tout entier n superieur ou égal à 1, on
pose tn = 160 - Vn.
a) Pour tout entier n supérieur ou égal à 1,
nous avons :
tn+1 = 160 - Vn+1 = 160 - (¼Vn + 120) = 40 - ¼Vn
= ¼(160 - Vn) = ¼tn.
Nous pouvons déduire de ce résultat que la suite (tn) est géométrique
de raison ¼ et de premier terme t1 = 160 - V1, soit t1
= 40.
b) Puisque (tn) est géométrique
de raison ¼ et de premier terme t1 = 40, nous avons, pour tout entier
n supérieur ou égal à 1, tn = 40×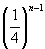 .
.
D'autre part, nous avons, pour tout entier n supérieur ou égal à 1, Vn
= 160 - tn, donc Vn = 160 - 40×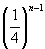 .
.
c) Nous savons que 0< ¼ <1, donc
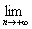
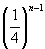 = 0.
= 0.
Par suite, nous avons
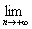 tn = 0.
tn = 0.
Or, pour tout entier naturel strictement positif, Vn = 160 - tn,
donc
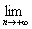 Vn = 160.
Vn = 160.
 Exercice 3
Exercice 3
1. La population de la ville A compte 200 000
habitants au 1er janvier 1995 et diminue de 3% par an.
Au 1er janvier 1996, sa population est donc de : 200 000 - (3/100)×
200 000 = 194 000 habitants,
et au 1er janvier 1997 de :
194 000- (3/100)×194 000 = 188 180 habitants.
De la même façon, la population, au 1er janvier 1995, de la ville B
est de 150 000 habitants et celle-ci augmente de 5% par an.
Au 1er janvier 1996, sa population sera donc de :
150 000 + (5/100)× 150 000 = 157 500 habitants,
et au 1er janvier 1997 de :
157 500 + (5/100)× 157 500 = 165 375 habitants.
2. a) Soit an la population de la
ville A au 1er janvier de l'année (1995 + n), n désignant un entier naturel
quelconque.
La population an+1 au 1er janvier de l'année (1995 + n +
1) est donnée par : an+1 = an - (3/100)an,
soit an+1 = (97/100)an ou an+1 = 0,97an
pour tout entier naturel n.
La suite (an) est géométrique de raison 0,97 et de premier terme a0
= 200 000.
bn désignant la population de la ville B au 1er janvier de
l'année (1995 + n), nous avons, au 1er janvier de l'année (1995 + n +
1) :
bn+1 = bn + (5/100)× bn = 1,05 bn
pour tout entier naturel n.
La suite (bn) est géométrique de raison 1,05 et de premier terme b0
= 150 000.
b) Nous pouvons déduire des résultats
précédents que, pour tout entier naturel n,
an = 200 000×(0,97)n et bn = 150 000×(1,05)n.
c) La population de la ville B est supérieure à
celle de la ville A au 1er janvier (1995 + n) lorsque bn an.
an.
Or, bn an
équivaut à 150 000×(1,05)n
an
équivaut à 150 000×(1,05)n
 200 000×(0,97)n
200 000×(0,97)n
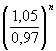

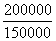
(1,08247)n
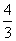
Mais la fonction ln est strictement croissante sur ]0 ; + [
donc :
[
donc :
n ln(1,08247) ln
ln
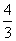
Donc n 
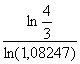 ,
puisque ln(1,08247)>0.
,
puisque ln(1,08247)>0.
Comme
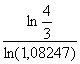 = 3,36 à 10-2 près et que n est un entier, nous devons donc avoir n
supérieur ou égal à 4.
= 3,36 à 10-2 près et que n est un entier, nous devons donc avoir n
supérieur ou égal à 4.
Donc, la population de la ville B est pour la première fois supérieure à
celle de la ville A au 1er janvier de l'année 1999.

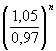
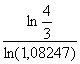 ,
puisque ln(1,08247)>0.
,
puisque ln(1,08247)>0.