Calculer la dérivée des fonctions
1° En développant
2° En utilisant le théorème de la dérivée des fonctions composées.
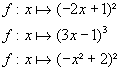
|
FONCTIONS |
Exercice 1
Dérivée d'une fonction composée
Calculer la dérivée des fonctions
![]()
1° En développant
![]() (x)
(x)
2° En utilisant le théorème de la dérivée des
fonctions composées.
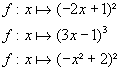
Exercice 2
Calculs de dérivées
Calculer la dérivée de la fonction
![]() en précisant
son ensemble de définition et celui de sa dérivée.
en précisant
son ensemble de définition et celui de sa dérivée.
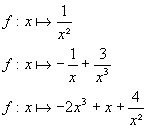
Exercice 3
Dérivées successives
Calculer les dérivées d'ordre 1 à n , n![]()
![]() *,
de
*,
de ![]() sur
l'intervalle I en utilisant éventuellement un raisonnement par récurrence.
sur
l'intervalle I en utilisant éventuellement un raisonnement par récurrence.
|
|
I=3. |
|
|
I=]2 ;+ |
|
|
I=3. |
Exercice 4
Tangentes
Pour chacune des fonctions suivantes, écrire une équation de la tangente au
point A d'abscisse a de la représentation graphique de la fonction
![]() .
.
|
|
pour a=-1, a=2 et a=3. |
|
|
pour a=-4, a=1 et a=2. |
|
|
pour a=0, a= |
Exercice 5
Asymptotes
Pour chacune des fonctions, écrire des équations des asymptotes parallèles aux
axes.
![]()
![]()
![]()
![]()
![]()
![]()
Exercice 6
Limites
Calculer les limites suivantes en justifiant les résultats
![]()
![]()
![]()
![]()
![]()
Exercice 7
Périodicité
Trouver une période pour chacune des fonctions suivantes :
![]()
![]()
![]()
![]()
Exercice 8
Symétries
Un repère orthogonal du plan est donné. Pour chacun des cas suivants, montrer
que la droite D est axe de symétrie de la représentation graphique de
![]() .
.
|
|
D : x = 1 |
|
|
D : x = 1 |
|
|
D : x = -1 |
|
|
D : x =
|
Exercice 9
Equations trigonométriques
Dans chaque équation, l'inconnue x est une mesure d'angle en radians.
Résoudre ces équations dans
![]() et représenter leurs
solutions par des points du cercle trigonométrique.
et représenter leurs
solutions par des points du cercle trigonométrique.
![]()
![]()
![]()
![]()
![]()
![]()
Exercice 10
Inéquations trigonométriques
Résoudre chacune des inéquations suivantes dans l'intervalle [0 ;2![]() [.
[.
La résolution sera fondée sur l'observation du cercle trigonométrique
![]()
![]()
![]()
![]()