Exercice 1
Soit la fonction f définie sur I par son expression f(x) en fonction de x. Dresser le tableau de signes de f(x).
1. f(x) = (x + 1)(5 - x) ; I =
2. f(x) = ; I = ]-; 2[]2; +[

 Exercice 2
Résoudre dans l'équation suivante : (2x + 3)² = (2x + 3)(x - 4).

 Exercice 3
Résoudre dans l'inéquation : .

 Exercice 4
Soit la fonction f définie sur I par son expression en fonction de x. A l'aide d'un tableau, étudier le signe de f(x).
1. I = ]-; -2[ ; f(x) =
2. I = ]-; -1[]-1; +[ ; f(x) =

 Exercice 5
Soit la fonction f définie sur la réunion d'intervalles ]-; -1[]-1; +[ par : f(x) = .
1. Ecrire f(x) sous la forme d'un seul quotient.
2. Dresser le tableau du signe de f(x).

 Exercice 1
1. Etudions le signe de chacun des facteurs :
Signe de (x + 1) : (x + 1) est positif pour x > -1.
Signe de (5 - x) : (5 - x) est positif pour x < 5.
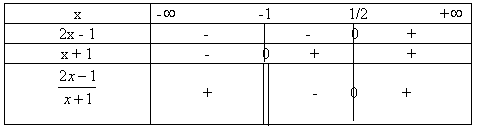
Dressons le tableau de signes :

 

2. Déterminons les signes des quotient et numérateur :
Signe de (3x + 1) : (3x + 1) est positif pour x > (-1/3)
Signe de (x - 2) : (x - 2) est positif pour x > 2
D'où le tableau de signes suivant :

 

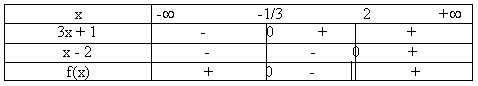
 Exercice 2
(2x + 3)² - (2x + 3)(x - 4) = 0
ce qui est équivalent à : (2x + 3)(2x + 3 - x + 4) = 0
ce qui est équivalent à : (2x + 3)(x + 7) = 0
Les solutions sont -3/2 ou -7.

 Exercice 3
est équivalent à : 0
qui est équivalent à :
qui est équivalent à :
Et on étudie le signe de ce quotient :

 

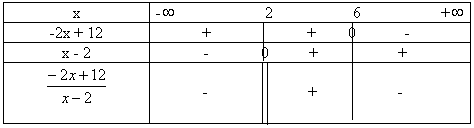
L'ensemble des solutions est : ]-; 2 [[6 ; +[.

 Exercice 4
1.
 

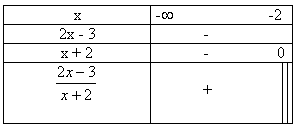
2.
 

 Exercice 5
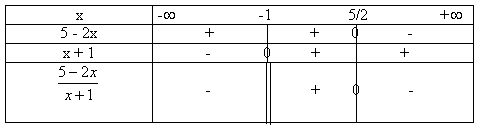
1. f(x) =
2. Le tableau de signes est le suivant :