Exercice 1
Dans chaque cas une des réponses au moins est exacte.
1. Le nombre 0 ! :
   a) est égal à 0
   b) est égal à 1
   c) n'a pas été défini

2. Le nombre de listes à k éléments distincts ou non, dans un ensemble à p éléments :
   a) est égal à k^p
   b) est égal à p^k
   c) est égal à

3. n et p sont deux nombres entiers naturels non nuls et p est inférieur ou égal à n.
   a) On a toujours
   b) On a toujours
   c) Il n'y a pas de relation générale entre et n^p

4. L'expression
   a) est la valeur de
   b) est la valeur de
   c) est la valeur de

5. On place 5 croix et 5 ronds dans une liste de 10 caractères. De combien de manières différentes peut-on placer ces éléments :
   a) 2¹⁰
   b)
   c)
6. Le nombre 4! représente :
   a) le nombre de classements possibles dans un ensemble à 4 éléments
   b) le nombre des permutations possibles dans un ensemble à 1 élément
   c) le nombre des arrangements des 4 éléments dans un ensemble de cardinal égal à 4.

 Exercice 2
On a représenté sur le diagramme ci-dessous un ensemble E et deux de ses sous-ensembles A et B (chaque élément de E est représenté par une croix).
 

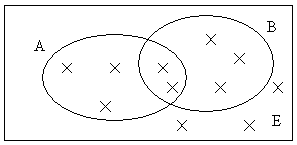
1. Calculer card(A), card(B), card(AB), card(AB), card(E).
2. Quelle égalité lie les quatre premiers nombres ?

 Exercice 3
Une urne contient 5 boules rouges, 4 noires, 3 vertes. On tire trois boules dans cette urne, successivement, en remettant chaque boule tirée dans l'urne avant de prendre les suivantes.
1. Quel est le nombre de tirages possibles ?
2. Calculer la probabilité :
   a) d'obtenir trois boules rouges ;
   b) d'obtenir deux boules rouges exactement ;
   c) d'obtenir au moins une boule rouge ;
   d) d'obtenir deux boules vertes et une noire ;
   e) d'obtenir trois boules de la même couleur ;
   f) d'obtenir trois boules de trois couleurs différentes.

 Exercice 4
Trois options sont offertes aux élèves d'une classe : espagnol, latin, musique. Chaque élève choisit une ou deux options. Le schéma ci-dessous indique le nombre d'élèves pour chaque combinaison d'options possible.
 

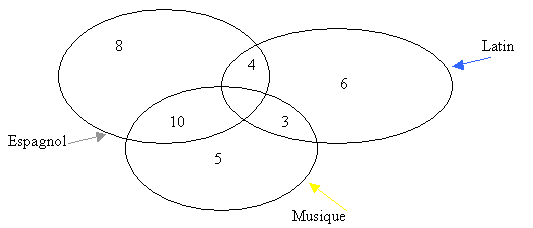
On choisit un élève au hasard dans cette classe.
Déterminer la probabilité des événements suivants :
1. l'élève étudie l'espagnol,
2. l'élève étudie uniquement l'espagnol,
3. l'élève étudie l'espagnol et le latin,
4. l'élève étudie l'espagnol ou le latin,
5. l'élève étudie uniquement une des deux langues : espagnol ou latin (il peut éventuellement faire aussi de la musique),
6. l'élève étudie une seule des trois options.

 Exercice 5
Une urne contient cinq boules blanches et trois boules rouges indiscernables au toucher.
1. On tire successivement sans remise trois boules dans l'urne.
   a) Combien y a-t-il de tirages possibles ?
   b) Quelle est la probabilité d'obtenir trois boules rouges ?
   c) Quelle est la probabilité d'obtenir deux boules rouges ?
2. Reprendre la première question, en supposant que les trois boules sont tirées simultanément. Comparer les résultats obtenus dans les deux questions.

 Exercice 6
On rappelle qu'une anagramme d'un mot est un mot qui contient les mêmes lettres (éventuellement répétées le même nombre de fois). Par exemple REVISE et SERVIE sont des anagrammes de EVIERS, on considère que ESEIVR en est une autre, bien que ce mot n'ait aucun sens.
1. Combien CHERS a-t-il d'anagrammes ?
2. Combien CHERE a-t-il d'anagrammes ?
3. Combien CHERCHER a-t-il d'anagrammes ?
4. Combien RECHERCHER a-t-il d'anagrammes ?

 Exercice 7
Une agence de voyages propose un circuit touristique comprenant quatre des douze capitales de la Communauté économique européenne (CEE).
Pour définir un circuit, on suppose que chaque capitale n'est visitée qu'une fois et on tient compte de l'ordre de visite de ces capitales ; par exemple, le circuit : " Paris, Madrid, Rome, Athènes " diffère du circuit : " Athènes, Rome, Paris, Madrid ".
1. Combien y a-t-il de circuits différents ?
Dans la suite, on suppose que chaque capitale a la même probabilité d'être choisie.
2. Calculer la probabilité de l'événement suivant : le circuit commence à Paris. (Le résultat de cette question sera donné sous forme de fraction irréductible).
3. Si le circuit commence à Paris, quelle est la probabilité pour que Madrid et Rome fassent partie du circuit ? (Ce résultat sera donné sous forme de fraction irréductible).

 Exercice 1
1. b)
2. b)
3. a) et b)
4. a) et b)
5. c)
6. a) et b) et c)

 Exercice 2
1. card(A) = 5, card(B) = 5, card(AB) = 2, card(AB) = 8, card(E) = 11.
2. L'égalité liant les quatre premiers nombres est la suivante : card(AB) = card(A) + card(B) - card(AB).

 Exercice 3
1. le nombre de tirages possibles est : 12³ = 1728
2. La probabilité :
   a) d'obtenir trois boules rouges est : 5³/12³ ;
   b) d'obtenir deux boules rouges exactement est : (5×5×7 + 5×7×5 + 7×5×5) / 1278 = 525 / 1728 ;
   c) d'obtenir au moins une boule rouge est: 1 - (7³ / 12³) = 1385 / 1728 ;
   d) d'obtenir deux boules vertes et une noire est : (3×3×4 + 3×4×3 + 4×3×3) / 1728 = 108 / 1728 ;
   e) d'obtenir trois boules de la même couleur est : (5³ + 4³ + 3³) / 1728 = 216 / 1728 ;
   f) d'obtenir trois boules de trois couleurs différentes est : (5×4×3×6) / 1728 = 360 / 1728.

 Exercice 4
La classe comprend 36 élèves.
1. Le nombre d'élèves étudiant l'espagnol est égal à : 8 + 4 + 10 = 22. Si on choisit un élève au hasard, la probabilité pour qu'il étudie l'espagnol est donc égale à : 22 / 36 (= 11 / 18).
2. Le nombre d'élèves étudiant uniquement l'espagnol est égal à 8. Si on choisit un élève au hasard, la probabilité pour qu'il étudie uniquement l'espagnol est donc égale à 8 / 36 (= 2/9).
3. Le nombre d'élèves étudiant l'espagnol et le latin est égal à 4. Si on choisit un élève au hasard, la probabilité pour qu'il étudie l'espagnol et le latin est donc égale à 4 / 36 (= 1/9).
4. Le nombre d'élèves étudiant l'espagnol ou le latin est égal à 8 + 10 + 4 + 3 + 6 = 31. Si on choisit un élève au hasard, la probabilité pour qu'il étudie l'espagnol ou le latin est donc égale à 31 / 36.
5. Le nombre d'élèves étudiant l'espagnol, l'espagnol et la musique, le latin, le latin et la musique est égal à 8 + 10 + 3 + 6 = 27. Si on choisit un élève au hasard, la probabilité pour qu'il étudie l'espagnol, l'espagnol et la musique, le latin, le latin et la musique est donc égale à 27 / 36 (= 3/4).
6. Le nombre d'élèves étudiant une seule des trois options est égal à 8 + 6 + 5 = 19. Si on choisit un élève au hasard, la probabilité pour qu'il étudie une seule des trois options est donc égale à 19 / 36.

 Exercice 5
1. a) Un tirage est constitué d'une suite de trois boules distinctes choisies parmi 8. Le nombre de tirages possibles est donc : = 336 (tous équiprobables).
   b) La probabilité d'obtenir trois boules rouges est : = 1/56.
   c) La probabilité d'obtenir deux boules rouges est :
Le nombre de façons de tirer successivement deux boules rouges distinctes est .
Le nombre de façons de tirer une boule blanche est .
le nombre de façons de placer deux boules rouges parmi trois positions est .
Donc, la probabilité cherchée est : = 15 / 56.
2. a) Un tirage revient à prendre trois éléments dans un ensemble à 8 éléments. Le nombre de tirages possibles est donc le nombre de parties à 3 éléments dans un ensemble à 8 éléments, c'est-à-dire .
Il y a donc 56 tirages possibles (tous équiprobables).
   b) La probabilité d'obtenir trois boules rouges est : = 1/56.
   c) La probabilité d'obtenir deux boules rouges est : = 15 / 56.
(où correspond au nombre de façons de tirer simultanément deux boules rouges et correspond au nombre de façons de tirer une boule blanche parmi 5 boules).
On peut remarquer que les résultats obtenus sont les mêmes que ceux de la question 1.

 Exercice 6
1. CHERS contient cinq lettres distinctes. Le nombre d'anagrammes est donc: 5! = 120.
2. CHERE contient aussi cinq lettres, mais il y a deux E. Notons les E₁ et E₂ pour commencer. Les classements RE₁CHE₂ et RE₂CHE₁ donnent le même mot.
D'une manière générale, toute anagramme est obtenue deux fois, une fois avec E₁ en premier, une fois avec E₂ en premier; le nombre d'anagrammes est donc égal au nombre de classements des cinq lettres, divisé par le nombre de classements des deux E.
Le nombre d'anagrammes de CHERE est égal à : (5!) / (2!) = 60.
3. CHERCHER contient huit lettres. On doit diviser 8! par (2!)⁴ (une fois parce qu'une permutation des deux E ne modifie pas une anagramme, une fois à cause des deux R, une autre à cause des deux C, une dernière à cause des deux H).
On a donc : (8!) / (2!)⁴ = 2 520 anagrammes.
4. RECHERCHER contient 10 lettres dont 3 R, 3 E, 2 C et 2 H. Le nombre d'anagrammes est donc :
(10!) / (3!×3!×2!×2!) = 25 200 anagrammes.

 Exercice 7
1. Un circuit correspond à un arrangement de 4 éléments de l'ensemble des 12 capitales de la C.E.E. (l'ordre intervient et les éléments doivent être distincts).
Le nombre des circuits est : = 11 880 circuits différents.
2. Chacune des capitales a la même probabilité d'être choisie en premier. Comme il y a 12 capitales, chacune d'entre elles, et en particulier Paris, a une chance sur 2 d'être la première étape du circuit.
La probabilité cherchée est donc : 1/12.
3. Le circuit commence à Paris.
le nombre de circuits possibles : il faut compléter par trois capitales distinctes en tenant compte de l'ordre dans lequel elles sont visitées.
Il y a donc = 990 circuits possibles.
circuits favorables : (P,R,M,X); (P,R,X,M); (P,M,R,X); (P,M,x,R); (P,X,R,M); (P,X,R,M).
Dans chacun des cas, il y a 9 circuits possibles (ce qui correspond au choix de la quatrième capitale). Le nombre de circuits favorables est donc : 9×6.
D'où : la probabilité cherchée est alors : (9×6) / (11×10×9) = 3 /55.